ChiefRunningPhist
Well-Known Member
The Brief:
They state: 3.03μmol/J
This calculates to: 80% efficiency
The datasheet calculates: 67.35% efficiency
What's the skinny: the difference is from the losses on the phosphor
The Claim:
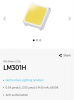
LM301H 6500K flux data:

LM301H 6500K testing parameters:
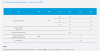
Digitized LM301H 6500K SPD:

The Breakdown:
The LM301H uses a blue base pump die with a peak of ~451nm. If phosphor conversion efficiency is 100%, which in real life it can approach but hasn't yet, then the max efficiency possible is ~3.77μmol/J.
(451nm) ÷ (119.6nm·J/μmol)
=
3.771μmol/J
The claim of 3.03μmol/J must then mean a total efficiency of 80.35%.
(3.03μmol/J) ÷ (3.771μmol/J)
=
0.8035; 80.35%
According to the digitized spectrum, the maximum lumen output per watt is ~342lm. If 342lm is multipled by the 80.35% efficiency calculated earlier via their 3.03μmol/J claim, a final lumen/w figure of ~275lm/w is achieved. This is greater than what they print in the data sheet.
(343.1lm/w) × (0.8035)
=
274.88lm/w
Looking at the flux characteristics of the best 6500K LM301H listed (SM bin), a maximum of 42lm per chip is printed. This equates roughly to 235lm/w.
(42lm) ÷ (0.065A × 2.75V)
=
234.97 lm/w
Looking at the printed calculation of ~235lm/w, and comparing with the digitized radiometric luminous efficacy of ~342lm/w, a total chip efficiency is calculated at 68.68%.
(234.97lm/w) ÷ (342.1lm/w)
=
0.6868; 68.68%
So which one is it? 68% or 80%?
Well I've since remebered lol Dammit! The discrepancy is due to 1 metric describing the power input vs the energy emitted after the phosphor losses, and the other metric is describing the power input vs the energy before the phosphor losses.
When I assume a CE of 1, I get ~3.3μmols/J. The stated claim is 3.03μmol/J, so I'm assuming the CE for the phosphor film they are using is not 1 but something close to 0.918. I'm going to wrestle a little more with this.
They state: 3.03μmol/J
This calculates to: 80% efficiency
The datasheet calculates: 67.35% efficiency
What's the skinny: the difference is from the losses on the phosphor
The Claim:

LM301H 6500K flux data:

LM301H 6500K testing parameters:

Digitized LM301H 6500K SPD:

The Breakdown:
The LM301H uses a blue base pump die with a peak of ~451nm. If phosphor conversion efficiency is 100%, which in real life it can approach but hasn't yet, then the max efficiency possible is ~3.77μmol/J.
(451nm) ÷ (119.6nm·J/μmol)
=
3.771μmol/J
The claim of 3.03μmol/J must then mean a total efficiency of 80.35%.
(3.03μmol/J) ÷ (3.771μmol/J)
=
0.8035; 80.35%
According to the digitized spectrum, the maximum lumen output per watt is ~342lm. If 342lm is multipled by the 80.35% efficiency calculated earlier via their 3.03μmol/J claim, a final lumen/w figure of ~275lm/w is achieved. This is greater than what they print in the data sheet.
(343.1lm/w) × (0.8035)
=
274.88lm/w
Looking at the flux characteristics of the best 6500K LM301H listed (SM bin), a maximum of 42lm per chip is printed. This equates roughly to 235lm/w.
(42lm) ÷ (0.065A × 2.75V)
=
234.97 lm/w
Looking at the printed calculation of ~235lm/w, and comparing with the digitized radiometric luminous efficacy of ~342lm/w, a total chip efficiency is calculated at 68.68%.
(234.97lm/w) ÷ (342.1lm/w)
=
0.6868; 68.68%
So which one is it? 68% or 80%?
Well I've since remebered lol Dammit! The discrepancy is due to 1 metric describing the power input vs the energy emitted after the phosphor losses, and the other metric is describing the power input vs the energy before the phosphor losses.
When I assume a CE of 1, I get ~3.3μmols/J. The stated claim is 3.03μmol/J, so I'm assuming the CE for the phosphor film they are using is not 1 but something close to 0.918. I'm going to wrestle a little more with this.
Attachments
-
857.9 KB Views: 13
Last edited: