How do you think this works with gene recombinations regarding flowering time and sativa percentage.
Say I cross 100 sativa x 100 indica which have 12 and 8 week flower times, respectively.
And get F1, 50/50 with 10 week flower time. Crossing F1 back with the sativa parent, would I get 75/25 sativa Dom with 11 week flowering time?
Edit: I'm trying to make sure I've got all this straight

Short Answer:
Yes, you would get an increasing ratio of sativa expressions as you continue to backcross to the sativa. Recombination dynamics and how they relate to a specific trait (flowering time), is dependent on whether or not the alleles that influence this trait are subject to cross over. Also, the simple model assumes the alleles are independently assorted and not linked. If flowering time genetic material suffers recombination, then you will get offspring that don’t follow the assumed ratios you expect from the simple Punnett Square model of anchored alleles.
Long Answer:
To better understand how recombination would nuance our model, we would have to also take into account the main assumption in our Mendelian model, independent assortment. This concept embodies the assumption that every allele pair separates independently during gamete formation. For example, let’s assume our female is short/quick flower and our male is tall/long flower. We could assume an even contribution of each possible trait in the formation of gametes.
Independent assortment would assume that his tall height is not affected by his long flower time and these traits can be treated as two independent probable expressions that can be observed in progeny with an even distribution. This means that during meiosis, the gametes (pollen grains in the case of our male) could split and create evenly distributed genotypes with 25% distribution among them. The progeny when combined with mother gametes, would show recombinant genes due to independent assortment combinations.
What would happen if these two traits are actually located on the same chromosome and thus are linked such that they cannot “pass” independently of one another? In this case, our male with alleles that are linked such that all tall plants are also long flowering [AB] and all short plants are fast flowering [ab], could only create these two possible gametes to create new offspring. This linkage actually makes the Punnett Square easier to deal with, as we do not have to evaluate every possible combination since we are limited in the pairings.
So now that we understand that some traits could be linked on the same chromosome and do not necessarily exhibit
[A1]independent assortment, we can see how recombination can further nuance this process. I assume the recombination you are asking about is the crossover recombination of linked traits as this provides a source of uncertainty.
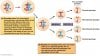
The process here is meiosis. Meiosis is a cell division process whereby the genetic contribution of a parent is “prepared” readying a gamete, or half of total genetic information for one new organism. The two halves of the parents will create one whole offspring during sexual reproduction.
You can see the recombination of the red/blue segments of the chromosomes that will produce recombinant gametes. When looking at the last column of gametes, realize that this means that the male pollen will have some ratio of these contributing genotypes. So for instance, each grain of pollen would have EITHER (AB) or (Ab) or (aB) or (ab). What percentage of pollen grains has either arrangement will depend on the recombination frequency. The frequency of this phenomenon is not set in stone for every instance, but you can use the results of your cross to attempt to establish this frequency.
Let’s assume you have a 20% recombination frequency. You would have pollen grains that exhibit 80% of parent genotypes (AB) and (ab). Assuming these occur with even distribution, 40% of pollen grains will have (AB) and 40% of pollen grains will have (ab). Now the recombinant possibilities are (Ab) and (aB) occurring with 20% frequency. Again, assuming even distribution, that means 10% of pollen grains have (Ab) and 10% have (aB). This would mean that the Punnett Square assumption of even distribution of all possible gamete permutations is no longer valid since we clearly have differing abundance of the possible genetic contributions owing to linked trait recombination frequency.
The assumptions of the independent assortment model (
the original model that sparked your question) would assume the increased genetic contribution from the plant that is being backcrossed in a predictable ever-converging manner. This increase does not take into account any recombinant dynamic or linked traits, but is a solid start that can serve as a guide. It is possible to calculate the recombination frequency for further work by comparing the expected phenotype distribution and the observed distribution using some statistical tools. Either way, the at home breeder can still benefit from the more simplistic models and working the statistical probabilities in their favor through understanding, careful observation, and benchmarking parent plants to establish genotype for a few traits.



 Edit: I really fragged the bitch today with it.
Edit: I really fragged the bitch today with it.

